ども、Tです。
何十年も前にやりつくされた議論ですが、今回は「どの断面が効率的か?」ということを考察していきます。本当は、直感的に理解できれば良いのですが。
というわけで今回は、効率的な部材断面は何かという観点で、四角形~H型(ウェブ無し)の7種類を整理しました。
効率的な部材の定義について考えた。
効率的な部材の整理方法ですが、まず断面二次モーメントI、断面係数Z,断面二次半径iが全ての種類で同じ値になるように、幅やせいを決めます。この時、断面積Aを算定しています。
断面は一様な材料(鋼)を使用すると考えれば、「断面積=メートル重量」と同義です。
さらに、「断面性能÷断面積」を計算してやれば、「同じ重量のとき、どの断面が効率的か?」という値が算出されます。
つまり、I/AとかZ/Aとかそんな値を、効率的な部材として定義し算定しました。
この値自体に意味はありませんので、あしからず。比較に意味があります。
断面二次モーメント 最も合理的な断面
「断面二次モーメント÷断面積」で比較したグラフが下図となります。最も合理的な断面は、H型鋼だと言えます。次いで、角型鋼管、鋼管。四角形、菱型、円柱、扇型の4種類はほぼ横並び。
柱、梁でもIは重要ですから、断面を小さくするならH型が効率的です。但し、柱の場合はX,Y方向加力を考えるのでH型は不利ですが。
断面係数 最も合理的な断面
同様に、断面係数を断面積で除した値を整理しました。この結果でも、先ほどのグラフと差異がありません。
1点、注意するのが四角形と菱型の違いです。断面二次モーメントは全く同じ値になる両者ですが、断面係数は菱型が4割程度小さくなります。
それはIの値が同じでも、中立軸から縁端までの距離が√2倍大きいからです。
つまり変形に対する性能は同じだが、応力に対する性能が落ちる、ということです。斜め方向加力の矩形柱に注意するのも、そのためです。
最後に、断面二次半径の比較です。H型鋼が特筆して大きいのですが、この値には意味がありません。つまり強軸方向の断面二次半径よりも弱軸回りのiが問題になるからです。
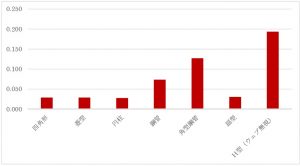
よって、iに関しては閉鎖断面の方が効果的で、角型鋼管を使用すれば、軸による値のバラつきがありません。例えば耐風梁に用いる際、H型鋼は中間に座屈止めが無いと座屈耐力を期待できませんが、角型鋼管ならスパンのまま飛ばせてしまいます。
まとめ
結局、僕たちが普段つかっているH型鋼と角型鋼管が最強でした。四角形と菱型の違いに注意ですね。
何度も言いますが、これらを直感で理解できると良いですよね。その助けになる本書。数式を使わず直観力が鍛えられる。本書を読めば、実務で10年は役立ちますよ。